메모리 계층 구조
"CPU에 얼마나 가까운가" 를 기준으로 각기 다른 용량과 성능의 저장 장치들을 계층적으로 나타낸 구조
각 계층은 성능, 용량, 가격 측면에서 차이가 있으며, 이를 효율적으로 활용하여 최적의 성능을 달성할 수 있음
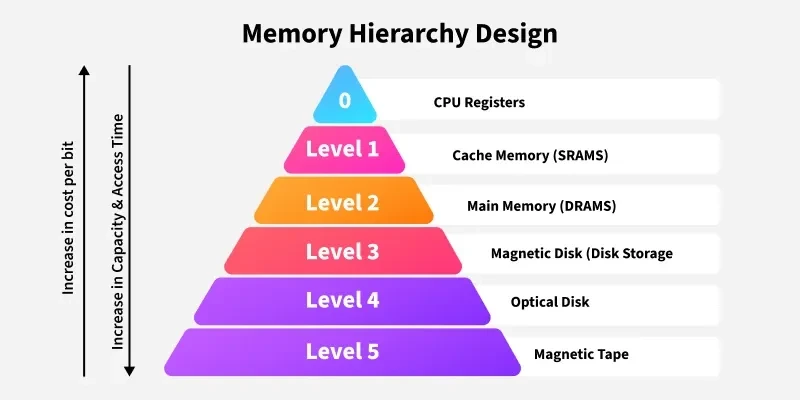
메모리 계층 구조의 원리
- CPU와 가까울수록 빠르다
- CPU 바로 옆에 있는 레지스터와 캐시 메모리는 매우 빠른 속도를 제공하지만, 용량이 작고 가격이 비쌉니다.
- 반면, RAM, SSD/HDD 등은 점점 CPU와 거리가 멀어지면서 속도가 느려지지만, 저장 용량이 커지고 가격이 저렴해집니다.
- 고속 메모리는 비싸고 용량이 작다
- 속도가 빠른 L1, L2, L3 캐시는 매우 비싸므로, CPU 내부에 소량만 탑재됩니다.
- 대용량 데이터를 저장하려면 상대적으로 느린 RAM이나 SSD를 활용해야 합니다.
- 느린 저장 장치는 용량이 크고 가격이 저렴하다
- 하드디스크(HDD)나 SSD 같은 저장 장치는 속도가 느리지만, 대용량 데이터를 저렴한 비용으로 저장할 수 있습니다.
- 클라우드 스토리지나 테이프 드라이브 같은 장치는 더욱 저렴한 비용으로 장기간 데이터를 보관하는 데 사용됩니다.
메모리 계층 구조의 단계
- 레지스터 (Register)
- CPU 내부에 위치하며, 가장 빠르고 가장 적은 용량(몇 바이트 수준)을 가짐
- 연산에 직접 사용되며, CPU 명령어를 처리하는 데 핵심 역할을 함
- 캐시 메모리 (Cache Memory - L1, L2, L3)
- CPU와 RAM 사이에 위치하며, 자주 사용되는 데이터를 미리 저장하여 빠르게 접근할 수 있도록 함
- L1 → L2 → L3 순으로 크기는 커지지만, 속도는 느려짐
- 메인 메모리 (RAM - Random Access Memory)
- 실행 중인 프로그램과 데이터를 저장하는 공간
- 캐시보다는 느리지만, 저장 용량이 크고 CPU와 직접 연결되어 빠르게 데이터 처리 가능
- 보조 저장 장치 (HDD, SSD)
- 영구적으로 데이터를 저장하는 장치
- RAM보다 속도가 훨씬 느리지만, 데이터가 전원이 꺼져도 유지됨
- 클라우드 스토리지, 테이프 드라이브
- 속도는 가장 느리지만, 대용량 데이터를 장기간 보관하는 데 최적화됨
- 백업 및 아카이빙 용도로 사용됨
참조 지역성 원리
참조 지역성(Locality of Reference)은 CPU가 메모리에 접근하는 패턴을 분석하여 최적의 성능을 이끌어내는 개념
이 원리를 기반으로 캐시 메모리가 동작하며, CPU가 자주 사용할 법한 데이터를 미리 로드하여 높은 캐시 적중률을 유지
참조 지역성은 크게 시간 지역성, 공간 지역성으로 구분함
- 시간 지역성 (Temporal Locality)
- 한 번 접근한 데이터나 명령어는 가까운 미래에 다시 접근될 가능성이 높음
- 이를 활용하여 캐시 메모리에 최근 사용한 데이터를 저장하여 성능을 향상시킴
- ex) for 루프 내 동일한 변수를 반복적 사용, 함수 호출 시 같은 변수가 조회됨
- 공간 지역성 (Spatial Locality)
- 특정 메모리 위치가 참조되면, 그 근처의 데이터도 곧 사용될 가능성이 높음
- 이를 기반으로 캐시나 RAM이 인접한 메모리 블록을 미리 로드하여 처리 속도를 높임
- ex 배열 순회, 코드 실행 등
참조 지역성 원리를 활용한 성능 최적화
- CPU 캐시 메모리 활용
- L1, L2, L3 캐시는 참조 지역성 원리를 기반으로 자주 사용하는 데이터를 저장하여 처리 속도를 높임
- 높은 캐시 적중률을 유지하면 CPU와 메모리 간 속도 차이를 해소할 수 있음
- 메모리 최적화 코딩 기법
- 배열을 순차적으로 접근하여 공간 지역성을 활용 (ex: Row-Major Order 방식)
- 자주 사용하는 변수를 캐시에 남도록 유지 (ex: 반복문에서 동일한 변수 활용)
- 운영체제의 페이지 캐싱 기법
- 운영체제는 참조 지역성을 활용하여 자주 사용하는 페이지를 미리 메모리에 적재
- 디스크 I/O를 최소화하여 성능을 개선
'CS' 카테고리의 다른 글
| [TIL] 명령어 집합 구조(ISA), CISC vs RISC (1) | 2025.03.13 |
|---|---|
| [TIL] 명령어 병렬 처리 기법 (파이프 라이닝, 슈퍼스칼라) (0) | 2025.03.13 |